Επόμενη: Λογική Πρώτης Τάξης Πάνω Επίπεδο: Εισαγωγή Προηγούμενη: Λογική 

2. Προτασιακή Λογική (Propositional Logic)

Η προτασιακή λογική είναι ένας φορμαλισμός κάποιων απλών μορφών συλλογιστικής. Είναι το απλούστερο λογικό σύστημα. Οι ισχυρισμοί αποτελούνται από προτάσεις οι οποίες είναι είτε αληθείς είτε ψευδείς αλλά όχι και τα δύο. Θα συμβολίζουμε τις προτάσεις με τους λατινικούς χαρακτήρες P, Q, R, κ.λ.π. και θα τις ονομάζουμε άτομα (atoms) ή ατομικούς τύπους (atomic formulas).

Για κάθε τυπική γλώσσα, πρέπει να οριστούν η σύνταξη (syntax) και η σημασιολογία (semantics) της. Η σύνταξη καθορίζει τις επιτρεπτές ακολουθίες συμβόλων (που θεωρούνται καλά σχηματισμένες) και η σημασιολογία καθορίζει τις μεταξύ τους σχέσεις. Η σύνταξη προϋποθέτει τον καθορισμό του αλφάβητου της γλώσσας, δηλαδή του συνόλου των συμβόλων με τα οποία μπορούν να κατασκευαστούν καλά σχηματισμένες ακολουθίες (λέξεις). Το αλφάβητο της προτασιακής λογικής αποτελείται από τα επόμενα σύμβολα:

• 'Ατομα, π.χ. P, Q, ή P₁, P₂, κ.λ.π.
• Πέντε λογικούς συνδέσμους:  (άρνηση),  (σύζευξη),  (διάζευξη),  (συνεπαγωγή),  (ισοδυναμία).
• Δύο σύμβολα στίξης: ``('' και ``)''.

'Ενας καλά σχηματισμένος τύπος (ή απλά τύπος), ορίζεται ως ακολούθως:

• Κάθε άτομο είναι τύπος (η απλούστερη μορφή).
• Αν  είναι τύπος τότε και ο  είναι τύπος (ο  προφέρεται ``όχι '').
• Αν  και  είναι τύποι, τότε και οι επόμενοι είναι (σύνθετοι) τύποι:
• , προφέρεται `` και ''
• , προφέρεται `` ή ''
• , προφέρεται `` συνεπάγεται '' ή ``αν  τότε ''
• , προφέρεται `` ισοδύναμο '' ή `` αν και μόνον αν ''
• Οι τύποι σχηματίζονται από τους τρεις παραπάνω κανόνες και μόνον αυτούς

Η σημασιολογία της προτασιακής λογικής αντιστοιχεί μία τιμή αληθείας (``αληθές'', ``ψευδές'' ή  αντίστοιχα) σ' έναν τύπο, βασισμένη σε μια ερμηνεία της γλώσσας. Μια ερμηνεία (interpretation) αντιστοιχεί τιμές αληθείας στα άτομα και επεκτείνεται σε σύνθετους τύπους με χρήση ενός πίνακα αληθείας (σχ.2α  ) για να μεταχειριστεί τους συνδέσμους. Για παράδειγμα, ο πίνακας αληθείας του τύπου  φαίνεται στο σχ. 2β .

  
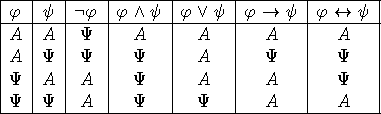
Σχήμα 2α: Ο πίνακας αληθείας για τους συνδέσμους της προτασιακής λογικής
 

  
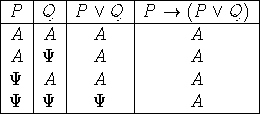
Σχήμα 2β: Ο πίνακας αληθείας για τον τύπο 
 

Κλείνουμε τη σύντομη εισαγωγή μας στην προτασιακή λογική, με τους ακόλουθους ορισμούς. 'Ενας τύπος F θα ονομάζεται ταυτολογία (tautology) ή έγκυρος (valid), αν είναι αληθής κάτω από οποιαδήποτε ερμηνεία. Αν ο τύπος F είναι ταυτολογία, γράφουμε . Για παράδειγμα, ο τύπος του πίνακα 2β , είναι μια ταυτολογία. 'Ενας τύπος θα ονομάζεται αντινομία (contradiction), αν είναι ψευδής κάτω από οποιαδήποτε ερμηνεία. Αν ένας τύπος καθίσταται αληθής κάτω από μια ερμηνεία M, θα λέμε ότι ο F ικανοποιείται από την M ή ότι η M είναι ένα μοντέλο (model) του F.

Θα ονομάζουμε δύο τύπους F και G ισοδύναμους (equivalent) και θα γράφουμε , αν και μόνον αν οι πίνακες αληθείας τους συμπίπτουν κάτω από οποιαδήποτε ερμηνεία.

Τα επόμενα αξιώματα είναι χρήσιμα στην προτασιακή λογική:
 

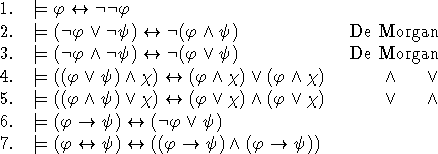
Τα αξιώματα 6 και 7 υπονοούν ότι το σύνολο των συνδέσμων  μπορεί να αντικαταστήσει όλους τους άλλους συνδέσμους ή, μ' άλλα λόγια, ότι το σύνολο αυτό είναι επαρκές.

'Ενας τύπος της μορφής  θα ονομάζεται διάζευξη (disjunction) των  κι ένας τύπος της μορφής  θα ονομάζεται σύζευξη (conjunction) των . Θα λέμε ότι ο τύπος F είναι σε Κανονική Διαζευκτική Μορφή - ΚΔΜ, αν έχει τη μορφή  και καθένα από τα F_i είναι σύζευξη λεκτικών στοιχείων (literals), όπου με τον όρο ``λεκτικό στοιχείο'' αναφερόμαστε είτε σ' ένα άτομο είτε στην άρνησή του. Θα λέμε ότι ο τύπος F είναι σε Κανονική Συζευκτική Μορφή - ΚΣΜ, αν έχει τη μορφή  και καθένα από τα F_i είναι διάζευξη λεκτικών στοιχείων.
 

Mon Apr 5 16:25:43 EEST 1999