Η λογική παρέχει έναν τρόπο για την αποσαφήνιση και την τυποποίηση της διαδικασίας της ανθρώπινης σκέψης. Μας
επιτρέπει να συλλογιζόμαστε (reason) για την ορθότητα των προγραμμάτων, να αναπαριστούμε προβλήματα
αλλά και να τα επιλύουμε. Η ανάγκη για μια τέτοια φορμαλιστική αναπαράσταση της ανθρώπινης σκέψης προήλθε
από το γεγονός ότι η φυσική γλώσσα, αν και ιδανική, είναι επίσης και βερμπαλιστική (verbose), ασαφής
(vague), πολυσήμαντη (ambiguous), περιέχει συμφραζόμενα (context sensitive), κ.α.
Η Μαθηματική Λογική έχει τις απαρχές της στην αρχαιότητα, στη θεωρία του Αριστοτέλη του Συλλογισμού
(syllogistic reasoning). Η μοντέρνα μαθηματική λογική ξεκίνησε με τις εργασίες των Descartes
(1596-1650) και Leibniz (1646-1716) και συνεχίστηκε από την εργασία του Boole επάνω στη
Μαθηματική Ανάλυση της Λογικής. Η Μαθηματική Λογική είναι η συστηματική μελέτη των έγκυρων ισχυρισμών
(valid arguments) με χρήση εννοιών από τα μαθηματικά. Ένας ισχυρισμός αποτελείται από συγκεκριμένες
δηλώσεις (ή προτάσεις), τις υποθέσεις (premises), από τις οποίες παράγεται μια άλλη δήλωση που
ονομάζεται συμπέρασμα (conclusion). Για παράδειγμα, ο επόμενος ισχυρισμός μας λέει ότι
Όλοι οι άνθρωποι είναι θνητοί,
Ο Σωκράτης είναι άνθρωπος,
επομένως, ο Σωκράτης είναι θνητός
Η Συμβολική Λογική είναι μια στενογραφία της κλασσικής λογικής. Οι ισχυρισμοί μελετώνται ανεξάρτητα από
την περιοχή από την οποία εκλέγονται. Αυτό επιτυγχάνεται εκφράζοντάς τους στη λογική ή συμβολική τους μορφή. Για παράδειγμα
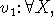άνθρωπος 
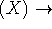θνητός (X),
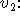άνθρωπος(Σωκράτης),
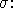θνητός(Σωκράτης)
ή
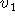και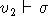 
,
όπου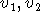 
είναι οι υποθέσεις μας, 
το συμπέρασμα και 
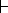είναι το σύμβολο της
(λογικής) συνεπαγωγής.