



Επόμενη: Σημασιολογία
Πάνω Επίπεδο: Εισαγωγή
Προηγούμενη: Προτασιακή Λογική (Propositional Logic)
Υπάρχουν προτάσεις που δεν μπορούν να εκφραστούν στην προτασιακή λογική. Η λογική πρώτης τάξης ή, όπως αλλιώς λέγεται, η
κατηγορηματική λογική (predicate logic), επεκτείνει την προτασιακή λογική εισάγοντας επιπρόσθετες έννοιες όπως τους
όρους (terms), τα κατηγορήματα (predicates) και τους ποσοδείκτες (quantifiers). Είναι
πολυπλοκότερη από την προτασιακή λογική και μπορεί να θεωρηθεί ως μια γενίκευση αυτής. Το σύνολο των συμβόλων της λογικής πρώτης
τάξης (το αλφάβητο πρώτης τάξης), ορίζεται ως ακολούθως:
- Σταθερές: a, b, c, a1, a2, κ.λ.π.
- Μεταβλητές:
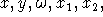 κ.λ.π.
κ.λ.π.
- Σύμβολα συναρτήσεων: f, g, κ.λ.π. Σε κάθε σύμβολο συνάρτησης αντιστοιχεί ένας αριθμός που ονομάζεται τάξη
(arity). Η τάξη ισούται με το πλήθος των ορισμάτων (arguments) ή, αλλιώς,
παραμέτρων (parameters), της συνάρτησης. 'Ετσι, έχουμε μοναδιαίες (unary)
συναρτήσεις (με ένα όρισμα), δυαδικές (binary) συναρτήσεις (με δύο ορίσματα) και, γενικά,
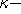 αδικές συναρτήσεις (με
αδικές συναρτήσεις (με  στο πλήθος ορίσματα).
στο πλήθος ορίσματα).
- Σύμβολα κατηγορημάτων: P, Q, κ.λ.π. Χρησιμοποιούνται για να δηλώνουν ιδιότητες σχέσεων. Κάθε σύμβολο κατηγορήματος έχει
μια συγκεκριμένη τάξη.
- Συνδέσμους:
 (άρνηση),
(άρνηση),  (σύζευξη),
(σύζευξη), 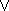 (διάζευξη),
(διάζευξη), 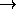 (συνεπαγωγή) και
(συνεπαγωγή) και
 (ισοδυναμία).
(ισοδυναμία).
- Δύο ποσοδείκτες:
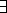 (υπαρξιακός ποσοδείκτης) και
(υπαρξιακός ποσοδείκτης) και 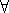 (καθολικός ποσοδείκτης).
(καθολικός ποσοδείκτης).
- Τρία σύμβολα στίξης: ``('', ``)'' και ``,''
Ας δούμε τώρα πώς ορίζονται οι όροι (terms):
- Μια σταθερά είναι όρος.
- Μια μεταβλητή είναι όρος.
- Αν f είναι μια n-αδική συνάρτηση και
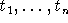 είναι n στο πλήθος όροι, τότε
είναι n στο πλήθος όροι, τότε 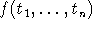 είναι όρος.
είναι όρος.
- Οι όροι κατασκευάζονται με τους τρεις παραπάνω κανόνες και μόνον αυτούς.
Θα ονομάζουμε καλά σχηματισμένους τύπους ή απλά τύπους, τις ``οντότητες'' που κατασκευάζονται από τους επόμενους κανόνες:
- Αν P είναι ένα
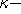 δικό κατηγόρημα και
δικό κατηγόρημα και 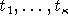 είναι
είναι  στο πλήθος όροι, τότε
στο πλήθος όροι, τότε
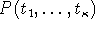 είναι ένας ατομικός τύπος (atomic formula) ή, απλά άτομο
(atom) ή θετικό λεκτικό στοιχείο (positive literal).
είναι ένας ατομικός τύπος (atomic formula) ή, απλά άτομο
(atom) ή θετικό λεκτικό στοιχείο (positive literal).
- Αν
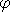 είναι τύπος, τότε και ο
είναι τύπος, τότε και ο 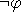 είναι τύπος.
είναι τύπος.
- Αν
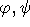 είναι τύποι, τότε και οι
είναι τύποι, τότε και οι 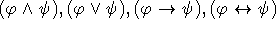 είναι τύποι.
είναι τύποι.
- Αν
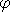 είναι τύπος και x μεταβλητή, τότε και οι
είναι τύπος και x μεταβλητή, τότε και οι 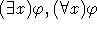 είναι τύποι.
είναι τύποι.
- Οι τύποι κατασκευάζονται με τους τέσσερις παραπάνω κανόνες και μόνον αυτούς.
Το σύνολο όλων των καλά σχηματισμένων τύπων που μπορούν να κατασκευαστούν από τα σύμβολα του αλφάβητου πρώτης τάξης, ονομάζεται
γλώσσα πρώτης τάξης.
Στους τύπους 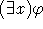 και
και 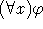 , το
, το 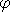 ονομάζεται εμβέλεια (scope) των ποσοδεικτών
ονομάζεται εμβέλεια (scope) των ποσοδεικτών 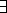 και
και
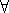 . Για παράδειγμα, η εμβέλεια του ποσοδείκτη
. Για παράδειγμα, η εμβέλεια του ποσοδείκτη 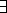 στον τύπο
στον τύπο 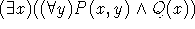 είναι ο τύπος
είναι ο τύπος
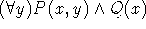 , ενώ η εμβέλεια του
, ενώ η εμβέλεια του 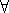 είναι ο τύπος P(x, y).
είναι ο τύπος P(x, y).
Μια εμφάνιση (occurrence) κάποιας μεταβλητής αμέσως μετά τον ποσοδείκτη και μέσα στην εμβέλειά του, ονομάζεται δεσμευμένη
(bound), ενώ η εμφάνισή της έξω από την εμβέλεια οποιουδήποτε ποσοδείκτη, ονομάζεται ελεύθερη (free). Για
παράδειγμα, η εμφάνιση της x στον τύπο 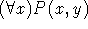 είναι δεσμευμένη, ενώ η εμφάνιση της y στον ίδιο τύπο, είναι ελεύθερη. 'Ενας
τύπος που στερείται ελεύθερων μεταβλητών θα ονομάζεται κλειστός τύπος (closed formula).
είναι δεσμευμένη, ενώ η εμφάνιση της y στον ίδιο τύπο, είναι ελεύθερη. 'Ενας
τύπος που στερείται ελεύθερων μεταβλητών θα ονομάζεται κλειστός τύπος (closed formula).
Βασικός όρος (ground term) (ή τύπος), είναι ένας όρος (ή τύπος) που δεν περιέχει καμία μεταβλητή. Για παράδειγμα, ο όρος
f(a, b) και ο τύπος Q(a, g(b, c)) είναι βασικοί, ενώ ο όρος f(a, x) αλλά και ο τύπος 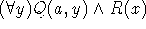 δεν είναι.
δεν είναι.
Εργαστήριο Γλωσσών Προγραμματισμού και Τεχνολογίας Λογισμικού
Mon Apr 5 16:25:43 EEST 1999
![]() και
και ![]() , το
, το ![]() ονομάζεται εμβέλεια (scope) των ποσοδεικτών
ονομάζεται εμβέλεια (scope) των ποσοδεικτών ![]() και
και
![]() . Για παράδειγμα, η εμβέλεια του ποσοδείκτη
. Για παράδειγμα, η εμβέλεια του ποσοδείκτη ![]() στον τύπο
στον τύπο ![]() είναι ο τύπος
είναι ο τύπος
![]() , ενώ η εμβέλεια του
, ενώ η εμβέλεια του ![]() είναι ο τύπος P(x, y).
είναι ο τύπος P(x, y).
![]() είναι δεσμευμένη, ενώ η εμφάνιση της y στον ίδιο τύπο, είναι ελεύθερη. 'Ενας
τύπος που στερείται ελεύθερων μεταβλητών θα ονομάζεται κλειστός τύπος (closed formula).
είναι δεσμευμένη, ενώ η εμφάνιση της y στον ίδιο τύπο, είναι ελεύθερη. 'Ενας
τύπος που στερείται ελεύθερων μεταβλητών θα ονομάζεται κλειστός τύπος (closed formula).
![]() δεν είναι.
δεν είναι.