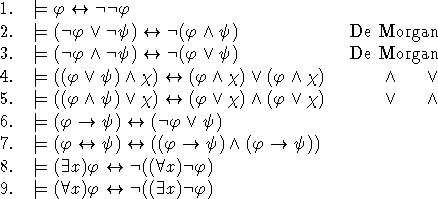Επόμενη: Κανονικές Μορφές
Πάνω Επίπεδο: Λογική Πρώτης Τάξης
Προηγούμενη: Σημασιολογία
Η ερμηνεία (interpretation) ορίζει την περιοχή της γλώσσας, απεικονίζει όρους της γλώσσας σε οντότητες της περιοχής και
αντιστοιχεί σε κάθε (κλειστό) τύπο μια τιμή αληθείας.
Μια ερμηνεία η οποία καθιστά έναν τύπο αληθή, ονομάζεται μοντέλο (model) γι' αυτόν τον τύπο. Μιλώντας φορμαλιστικά, αν
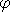 είναι ένας τύπος και M μια ερμηνεία, η M θα ονομάζεται μοντέλο του
είναι ένας τύπος και M μια ερμηνεία, η M θα ονομάζεται μοντέλο του 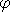 αν τον ικανοποιεί, αν, δηλαδή, τον καθιστά αληθή.
Θα λέμε τότε ότι o
αν τον ικανοποιεί, αν, δηλαδή, τον καθιστά αληθή.
Θα λέμε τότε ότι o 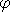 έχει την ερμηνεία M ως μοντέλο. Αν
έχει την ερμηνεία M ως μοντέλο. Αν 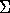 είναι ένα σύνολο τύπων και M μια ερμηνεία, η M θα
ονομάζεται μοντέλο του
είναι ένα σύνολο τύπων και M μια ερμηνεία, η M θα
ονομάζεται μοντέλο του 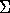 αν είναι μοντέλο κάθε τύπου
αν είναι μοντέλο κάθε τύπου 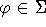 . Θα λέμε τότε ότι το
. Θα λέμε τότε ότι το 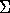 έχει για μοντέλο τη M.
έχει για μοντέλο τη M.
Δίνουμε τώρα τους επόμενους ορισμούς:
- Λέμε ότι ο τύπος
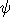 προκύπτει (λογικά) από τον
προκύπτει (λογικά) από τον 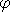 και γράφουμε
και γράφουμε 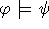 , αν κάθε μοντέλο του
, αν κάθε μοντέλο του
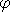 είναι και μοντέλο του
είναι και μοντέλο του 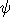 .
.
- Λέμε ότι οι τύποι
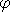 και
και 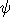 είναι (λογικά) ισοδύναμοι και γράφουμε
είναι (λογικά) ισοδύναμοι και γράφουμε 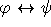 ,
αν
,
αν 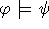 και
και 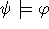 , δηλαδή αν κάθε μοντέλο του
, δηλαδή αν κάθε μοντέλο του 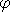 είναι και μοντέλο του
είναι και μοντέλο του 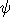 .
.
- Θα λέμε ότι ο τύπος
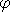 είναι έγκυρος (valid) ή ταυτολογία (tautology) και θα γράφουμε
είναι έγκυρος (valid) ή ταυτολογία (tautology) και θα γράφουμε
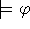 , αν ο
, αν ο 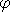 δέχεται κάθε ερμηνεία ως μοντέλο του. Στην αντίθετη περίπτωση θα τον ονομάζουμε
άκυρο (invalid).
δέχεται κάθε ερμηνεία ως μοντέλο του. Στην αντίθετη περίπτωση θα τον ονομάζουμε
άκυρο (invalid).
- Ο
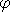 θα ονομάζεται ικανοποιήσιμος (satisfiable) ή συνεπής (consistent), αν υπάρχει
τουλάχιστον μία ερμηνεία που να τη δέχεται ως μοντέλο.
θα ονομάζεται ικανοποιήσιμος (satisfiable) ή συνεπής (consistent), αν υπάρχει
τουλάχιστον μία ερμηνεία που να τη δέχεται ως μοντέλο.
- Ο
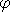 θα ονομάζεται ασυνεπής (inconsistent) ή ανικανοποίητος (unsatisfiable) ή
αντίθεση (contradiction), αν δεν δέχεται καμία ερμηνεία για μοντέλο του.
θα ονομάζεται ασυνεπής (inconsistent) ή ανικανοποίητος (unsatisfiable) ή
αντίθεση (contradiction), αν δεν δέχεται καμία ερμηνεία για μοντέλο του.
- Ο
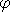 θα ονομάζεται απρόβλεπτος (contingent), αν είναι ικανοποιήσιμος αλλά όχι ταυτολογία.
θα ονομάζεται απρόβλεπτος (contingent), αν είναι ικανοποιήσιμος αλλά όχι ταυτολογία.
'Οπως και στην προτασιακή λογική, έτσι και στην λογική πρώτης τάξης έχουμε κάποιες ενδιαφέρουσες ταυτολογίες:
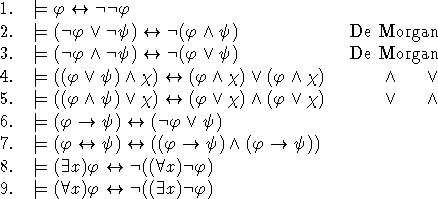
Οι ταυτολογίες 6, 7 δείχνουν ότι το σύνολο των συνδέσμων 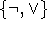 είναι επαρκές, ενώ οι δύο τελευταίες εκφράζουν την
δυϊκότητα των συμβόλων
είναι επαρκές, ενώ οι δύο τελευταίες εκφράζουν την
δυϊκότητα των συμβόλων 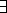 και
και 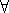 .
.
Εργαστήριο Γλωσσών Προγραμματισμού και Τεχνολογίας Λογισμικού
Mon Apr 5 16:25:43 EEST 1999
![]() είναι ένας τύπος και M μια ερμηνεία, η M θα ονομάζεται μοντέλο του
είναι ένας τύπος και M μια ερμηνεία, η M θα ονομάζεται μοντέλο του ![]() αν τον ικανοποιεί, αν, δηλαδή, τον καθιστά αληθή.
Θα λέμε τότε ότι o
αν τον ικανοποιεί, αν, δηλαδή, τον καθιστά αληθή.
Θα λέμε τότε ότι o ![]() έχει την ερμηνεία M ως μοντέλο. Αν
έχει την ερμηνεία M ως μοντέλο. Αν ![]() είναι ένα σύνολο τύπων και M μια ερμηνεία, η M θα
ονομάζεται μοντέλο του
είναι ένα σύνολο τύπων και M μια ερμηνεία, η M θα
ονομάζεται μοντέλο του ![]() αν είναι μοντέλο κάθε τύπου
αν είναι μοντέλο κάθε τύπου ![]() . Θα λέμε τότε ότι το
. Θα λέμε τότε ότι το ![]() έχει για μοντέλο τη M.
έχει για μοντέλο τη M.