Επόμενη: Και λίγη ...ιστορία Πάνω Επίπεδο: Λογικός Προγραμματισμός Επόμενη: Δομές Δεδομένων 

5.5 Το υπολογιστικό μοντέλο του Λογικού Προγραμματισμού

Η καρδιά του υπολογιστικού μοντέλου του λογικού προγραμματισμού είναι ο αλγόριθμος ενοποίησης (unification algorithm). Ο αλγόριθμος αυτός παίζει ένα κεντρικό ρόλο στην αυτοματοποιημένη απαγωγή (automated deduction) και στη χρήση της λογικής συνεπαγωγής (logical inference) στην τεχνητή νοημοσύνη. Θα παρουσιάσουμε με άτυπο τρόπο τον αλγόριθμο ενοποίησης στο λογικό προγραμματισμό, ακολουθώντας την ορολογία του τελευταίου.

Ονομάζουμε ενοποιητή (unifier) δύο όρων μια αντικατάσταση που αν εφαρμοστεί επάνω τους, τους καθιστά όμοιους. Ο γενικότερος ταυτοποιητής ή, σύντομα, mgu , δύο όρων, είναι εκείνος ο ενοποιητής που μετατρέπει το κοινό στιγμιότυπο (instance) των δύο όρων, στη γενικότερή του μορφή. Θα λέμε ότι ο όρος t είναι κοινό στιγμιότυπο των όρων t₁ και t₂, αν υπάρχουν αντικαταστάσεις  και  τέτοιες, ώστε . 'Ενας όρος u είναι γενικότερος από έναν όρο t, αν ο t είναι ένα στιγμιότυπο του u αλλά ο u δεν είναι στιγμιότυπο του t.

Λέμε ότι ένας αλγόριθμος υπολογίζει τον mgu δύο όρων, αν τερματίζει επιτυχώς ή αναφέρει την αποτυχία στην αντίθετη περίπτωση. Ας είναι V μια μεταβλητή και T ένας όρος. Ονομάζουμε έλεγχο εμφάνισης (occurs check), τον έλεγχο για το εάν η μεταβλητή V περιέχεται στον όρο T. Στο σχ. 5.5α  , συνοψίζονται οι κανόνες ενοποίησης.

  
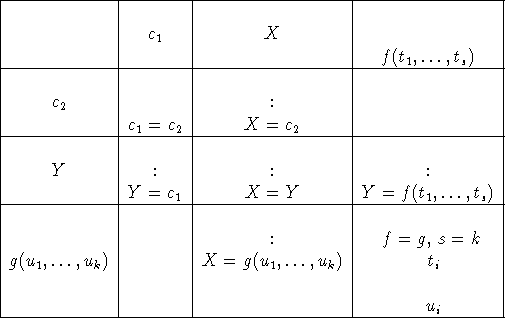
Σχήμα 5.5α: Οι κανόνες ενοποίησης
 

Για παράδειγμα, ο mgu των επόμενων όρων δίνεται στο σχ. 5.5β  .

  
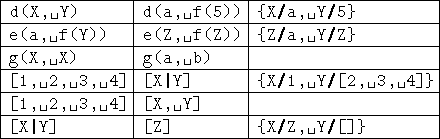
Σχήμα 5.5β: Παραδείγματα ενοποίησης
 

'Οταν υλοποιούμε τον αλγόριθμο υλοποίησης για μια συγκεκριμένη γλώσσα λογικού προγραμματισμού, οι λογικές μεταβλητές αλλά και άλλοι όροι, αναπαριστάνονται από θέσεις μνήμης (memory cells). Μια δέσμευση μεταβλητής (variable binding) υλοποιείται αντιστοιχώντας στη θέση μνήμης της μεταβλητής μια αναφορά, η οποία περιέχει την αναπαράσταση του όρου με τον οποίο έχει δεσμευτεί η συγκεκριμένη μεταβλητή.

'Οπως αναφέρθηκε και προηγουμένως, η αποδεικτική διαδικασία που χρησιμοποιείται για τα οριστικά, κι επομένως για τα λογικά, προγράμματα, είναι η SLD- ανάλυση (ή, ακριβέστερα, η SLDNF- ανάλυση). Μια SLDNF- άρνηση (ή υπολογισμός) ενός λογικού προγράμματος, ξεκινά από κάποιον αρχικό στόχο (ή ερώτημα) G και προσπαθεί να βρει μια απόδειξη για το στόχο αυτό. 'Ενα στιγμιότυπο (instance) του ερωτήματος για το οποίο έχει βρεθεί μια απόδειξη, είναι μια υπολογισμένη απάντηση (ή λύση) στο ερώτημα.

Ας είναι  ένα λογικό πρόγραμμα κι ένα αρχικό (πιθανώς συζευκτικό) ερώτημα G. Περιγράφουμε άτυπα, με χρήση της ορολογίας του λογικού προγραμματισμού, την SLD- ανάλυση για το .

1. Το αναλυθέν τίθεται ίσο με το G.
2. Επιλέγεται ένας στόχος G_i από το αναλυθέν.
3. Επιλέγεται μια (μετονομασμένη) πρόταση


από το , τέτοια ώστε τα G_i και C να ενοποιούνται με mgu . Αν δεν είναι δυνατό να βρεθεί μια τέτοια πρόταση, αναφέρεται αποτυχία.
4. Το G_i αντικαθίσταται από τη σύζευξη  (αναγωγή του G_i) και εφαρμόζεται ο  στο προκύπτον αναλυθέν.
5. Αν το αναλυθέν που προέκυψε από στο προηγούμενο βήμα δεν είναι η κενή πρόταση, επαναλαμβάνουμε τη διαδικασία από το βήμα 1, διαφορετικά επιστρέφεται ο mgu , ο οποίος είναι ο περιορισμός της σύνθεσης  στις μεταβλητές του G.

'Οπως αναφέρθηκε και στην περιγραφή του αλγορίθμου της SLD- ανάλυσης, η επιλογή του προς αναγωγή στόχου γίνεται από τον αλγόριθμο υπολογισμού (ή επιλογής) και, στην πραγματικότητα, είναι αυθαίρετη. Αν υπάρχει ένας επιτυχημένος υπολογισμός με την επιλογή ενός συγκεκριμένου στόχου, τότε υπάρχει ένας επιτυχής υπολογισμός οποιουδήποτε άλλου στόχου. Επιπρόσθετα, η επιλογή της πρότασης για την αναγωγή του επιλεγμένου στόχου, δεν είναι ντετερμινιστική. Η επιλογή της πρότασης επηρεάζει τον υπολογισμό, διότι δεν οδηγούν όλες οι επιλογές σε επιτυχείς υπολογισμούς. Για κάποιους υπολογισμούς, υπάρχει ακριβώς μία πρόταση στο πρόγραμμα που να μπορεί να ανάγει κάθε στόχο. Τέτοιοι υπολογισμοί ονομάζονται ντετερμινιστικοί.

'Ενας τρόπος για να βρούμε μια άρνηση, είναι το SLD- δέντρο. Αν θυμηθούμε την περιγραφή του, το SLD- δέντρο, ή απλά δέντρο αναζήτησης, ενός στόχου G ως προς το πρόγραμμα , είναι εκείνο το δέντρο στο οποίο

• Κάθε κόμβος είναι ένας (πιθανά συζευκτικός) στόχος και η ρίζα του δέντρου είναι ο στόχος G.
• Αν


είναι ένας κόμβος με επιλεγμένο υποστόχο A_s, για κάθε πιθανή αναγωγή του υποστόχου A_s, υπάρχει μια ακμή που οδηγεί σ' ένα κόμβο με το αναλυθέν, όπως αυτό δημιουργείται από το τέταρτο βήμα του αλγόριθμου ανάλυσης, που δώσαμε προηγουμένως. Είναι προφανές ότι υπάρχουν περιπτώσεις όπου από έναν κόμβο ξεκινούν περισσότερες από μία ακμές που οδηγούν σε διαφορετικά αναλυθέντα. Αυτό σημαίνει ότι υπάρχουν εναλλακτικές επιλογές για τον προς αναγωγή στόχο (μη-ντετερμινιστικός στόχος).

Υπάρχουν τριών ειδών κλαδιά:

• Κλαδιά επιτυχίας (success branches), τα οποία είναι μονοπάτια από τη ρίζα στην κενή πρόταση. Ενα τέτοιο κλαδί αντιστοιχεί σε μια άρνηση του G και μπορούμε να πάρουμε μια απάντηση.
• Κλαδία αποτυχίας (failure branches), τα οποία είναι μονοπάτια από τη ρίζα σε κάποιο φύλλο με μια μη-κενή πρόταση, από την οποία δεν είναι δυνατές περαιτέρω αναγωγές.
• 'Απειρα κλαδιά (infinite branches), τα οποία δεν οδηγούν πουθενά.

Ας θεωρήσουμε το επόμενο πρόγραμμα  και το στόχο G:
 

 
 

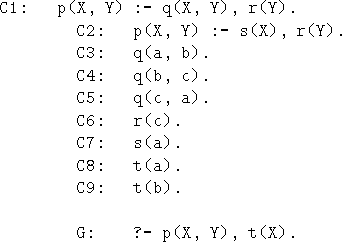
Το δέντρο αναζήτησης για το  στο οποίο επιλέγεται πάντοτε ο αριστερότερος στόχος, φαίνεται στο σχ. 5.5γ  .

  
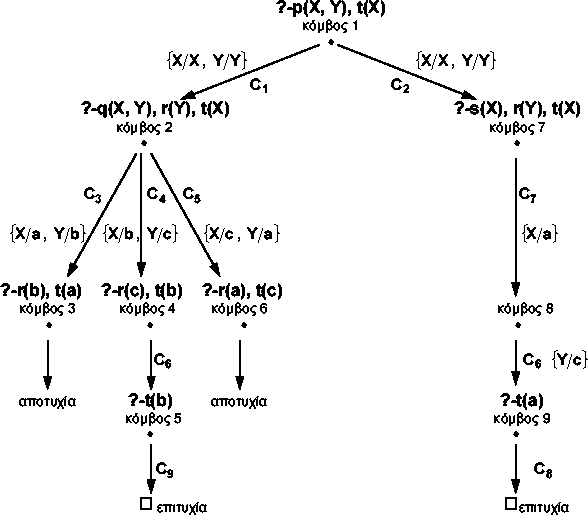
Σχήμα 5.5γ: SLD- άρνηση με επιλογή του αριστερότερου στόχου
 

Για να βρούμε όλες τις πιθανές απαντήσεις σ' ένα στόχο G, πρέπει να ερευνήσουμε ολόκληρο το δέντρο (όλα τα κλαδιά). Μια μέθοδος είναι η σε πλάτος-πρώτα (breadth-first) αναζήτηση, να εξερευνήσουμε, δηλαδή, όλα τα πιθανά μονοπάτια παράλληλα (σχ. 5.5δ ). Η μέθοδος αυτή διασφαλίζει την εύρεση πιθανών πεπερασμένων κλαδιών επιτυχίας.

  
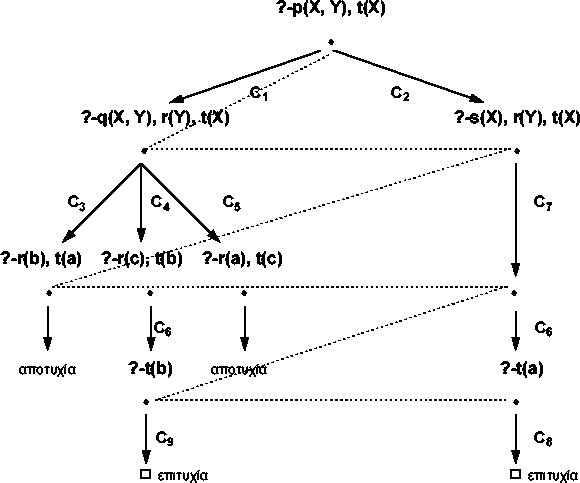
Σχήμα 5.5δ: Σε πλάτος-πρώτα αναζήτηση
 

Μια άλλη δυνατότητα που έχουμε είναι να εξερευνήσουμε το δέντρο αναζήτησης με χρήση της σε βάθος-πρώτα (depth-first) αναζήτησης (σχ. 5.5ε ). Αυτή η στρατηγική αναζήτησης δεν διασφαλίζει την εύρεση όλων των κλαδιών επιτυχίας, ακόμα κι αν υπάρχει ένα, αφού η αναζήτηση ενδέχεται να ``πέσει'' σ' ένα άπειρο μονοπάτι.

  
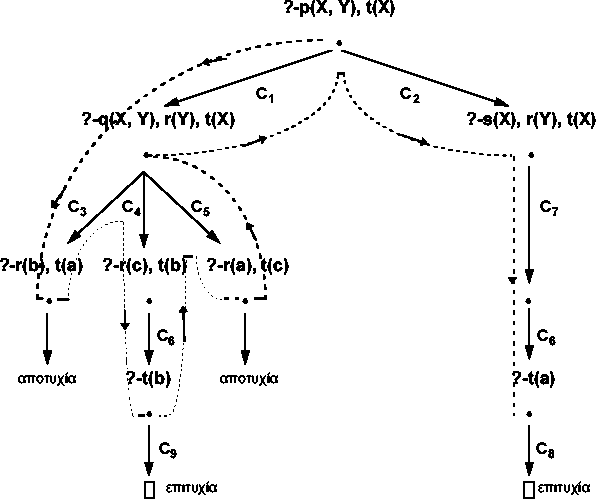
Σχήμα 5.5ε: Σε βάθος-πρώτα αναζήτηση
 

Συμπεραίνοντας, μπορούμε να πούμε ότι η σε πλάτος-πρώτα αναζήτηση είναι μια πλήρης αποδεικτική διαδικασία, ενώ η σε βάθος-πρώτα δεν είναι. Ωστόσο, για λόγους ευκολίας στην υλοποίηση, η γλώσσα λογικού προγραμματισμού Prolog χρησιμοποιεί τη σε βάθος-πρώτα στρατηγική, η οποία έχει αποδειχτεί, στην πράξη, επαρκής για αρκετές εφαρμογές. 'Αλλες γλώσσες λογικού προγραμματισμού χρησιμοποιούν διαφορετικές μορφές ελέγχου, όπως π.χ. η LOGLISP (Robinson και Sibert) η οποία εφαρμόζει σε πλάτος-πρώτα αναζήτηση στο δέντρο αναζήτησης, η IC-Prolog (Clark και McCade) που χρησιμοποιεί συνεργασία ρουτινών (co-routining), η MU-Prolog (Naish) που θέτει σε διαθεσιμότητα την εκτέλεση στόχων, κ.α.
 

Mon Apr 5 16:25:43 EEST 1999