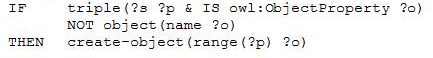This rule creates an object in the knowledge base of CLIPS. It searches for a triple that has the rdf:type property as predicate and checks if the class denoted by the object part of the triple exists in the system as materialized class (function class-exists) in order to be able to create the object ?s of this class type. Furthemore, it checks if the object ?s does not exist in the system as an already created object, otherwise it fails. The body of the rule creates the object ?o of class type ?s (function create-object). With this rule we achieve the materialization of a new instance with the condition that the corresponding class already exists in the knowledge base.

This rule has the same functionality to the previous one, but handles objects that are already created in the system. There are cases when an instance of the ontology is defined to have multiple class types. For example, a property may defined to be of type owl:ObjectProperty and owl:SymmetricProperty. If the system contained only Rule 1, then it would be infeasible to materialize the information of multiple class types, since it would create the instance as object of the first randomly selected class type and afterwards the rule would not be activated again (due to the NOT object(name ?s) constraint). Since multiple object types are not allowed in an object-oriented programming environment, we have implemented Rule 2 that operates as follows. Assuming that TypeA is the class of the already defined object and TypeB is the new class defined by the object part of the triple, initially the system performs a check to determine if TypeB is subclass of TypeA and changes object’s type to the class TypeB. Otherwise, the system checks if there is already a class subclass of the two class types only and changes the type of the object to this subclass. Otherwise it creates dynamically a class subclass of the two class types and changes the type of the object to this new subclass. In this way, the object obtains a new class type, preserving also the class type that already has. If TypeA is subclass of TypeB or the two class types are the same, the system does not perform any change. Here you can find a graphical representation of the previous procedure.

Rule 3 populates object properties with ontology values. It finds a triple with predicate a ?p property which should be an owl:ObjectProperty and checks if both subject and object of the triple exist in the knowledge base in the form of already materialized objects. Furthermore, the rules checks if the property denoted by the predicate of the triple exists in the class type of the object ?s and if the class type of the ?o is compatible with the class type (rdfs:range) of the property ?p. "Compatible" means that that the class type of ?o should be the same or subclass of the class denoted by the range constraint of the property ?p. In the body of the rule it inserts the value ?o in the slot ?p of the object ?s.

Rule 4 has the same functionality to Rule 3, but handles property values that are not compatible with the rdfs:range constaint of the property they are to be inserted. To handle such cases, we change the class type of the value ?o following the same methodology to Rule 2 in order to obtain also a new class type denoted by the rdfs:range constraint of the property ?p. After that, the rule inserts the value ?o into the slot ?p of the object ?s.

Rule 5 inserts values for datatype properties. It follows the same methodology to Rule 3, but ignores values that are not compatible with the rdfs:range constraint of the corresponding properties. For example, if a datatype property is declared to have integer type for range values and the object part of a triple denotes a string type, the triple is ignored.

Rule 6 handles triples that denote properties that are not existed in the class types of objects ?s and thus values ?o cannot be inserted. To handle such cases, we change the class type of the object ?s following the same methodology to Rule 2 in order for the object ?s to obtain a new class type, the class denoted by the rdfs:domain restriction of the property ?p.

Rule 7 has exactly the same functionality to Rule 6 but it handles datatype properties.

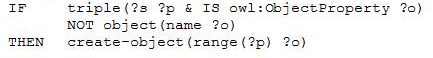
Rule 8 handles triples whose predicate ?p refers to an object property and the object ?o does not exist in the knowledge base. In this case, the rule creates an object with name ?o with the rdfs:range property value of ?p as its class type.

Rule 9 handles the case of class equivalence among actual (named) classes. The main idea is that a class meta-object is randomly selected in order to become the subclass of all its equivalent classes (and of its superclasses of course through its rdfs:subClassOf slot values). The rule finds a class meta-object with name ?c and retrieves its subclass values (list $?S) and its equivalent classes (list $?L) and performs the following tests: checks if the actual class ?c does not exist in the system as a materialized defclass construct, checks if the list $?L contains class meta-objects of actual (named) classes (it may contain also other values, such as restriction meta-objects), checks if the actual classes of the list $?L exist in the system as defclass constructs and finally checks if the list $?L is not subset of list $?S. The last check ensures that the rule will not be activated again, if already a class ?c is subclass of its equivalent classes. In the body of the rule, the class ?c is created as subclass of the union of the rdfs:subClassOf class values and the actual classes of the owl:equivalentClass slot. Furthermore, the sufficient information is inserted into c's sufficient slot (see Rule X).

Rule 10 handles the case of class equivalence between a named class and restriction classes. This case is handled by altering the owl:intersectionOf values of the named class. More specifically, the rule finds a class meta-object ?c and checks if the class ?c is not already materialized as defclass construct. Furthemore it checks if the list $?L of c's equivalent classes contains any restriction meta-object in order to be valid the activation of this rule. In the body of the rule, we copy all the restriction meta-objects of list $?L into c's owl:intersectionOf slot. In that way, class equivalance of this type is transformed into intersection information.

Rule 11 handles the case of class equivalence between a named class and anonymous classes (unnamed classes direct instances of owl:Class). The system handles this case in the same way as Rule 10, by altering the owl:intersectionOf slot values of the named class and inserting only the anonymous classes into it.

Rule 10 and Rule 11 change the equivalent class information of classes into intrersection information by altering the values of the owl:intersectionOf slot of a randomly selected class meta-object (Rule 9 creates directly the class). Thus, we have implemented Rule 12 in order to materialize the class information from the owl:intersectionOf slot. It finds a class meta-object named ?c that is not meterialized as defclass construct and checks if all of the classes in the list $?L (intersection classes) exist in the system. In the body of, the rule creates the actual class subclass of the union of the rdfs:subClassOf class values and the actual classes of the owl:intersectionOf slot. Furthermore, it inserts into c's rdfs:subClassOf slot the new superclasses.

Rule 13 is an example rule that handles the transitivity of the owl:equivalentClass property. The rule finds two class meta-objects ?n1 and ?n2, where ?n2 exists in the equivalent class list of ?n1. Moreover the rule checks if there is a need to be activated for this two class meta-objects through the function transitivity. This function checks if it is already computed the partial transitive closure of the two selected objects. In the body of the rule, the partial transitive closure is computed. Similar rules exist for every OWL built-in property that are declared as transitive, e.g. owl:equivalentProperty. The rule is similar in all cases, only the name of the property is changing.

Rule 14 is an example rule that handles the symmetry of the owl:equivalentClass property. The rule finds two class meta-objects ?n1 and ?n2, where ?n2 exists in the equivalent class list of ?n1. Moreover the rule checks if there is a need to be activated for this two class meta-objects through the function symmetry. This function checks if the ?n2 has already the value ?n1 in its equivalent class slot. In the body of the rule, the value ?n1 is inserted into ?n2's equivalent slot. Similar rules exist for every OWL built-in property that are declared as symmetric, e.g. owl:equivalentProperty. The rule is similar in all cases, only the name of the property is changing.

Rule 15 checks the domain and range values of inverse propertes. It finds a property object named ?p1 whith domain and range values the lists $?D1 and $?R1 respectively, which has an inverse property ?i. Then it locates the property object ?i and retrieves its doman and range values into the lists $?D2 and $?R2 respectively. It checks if the domain values of the one object property are not similar to the range values of the other and vice versa and in the body of the rule, it makes the appropriate changes in the lists.

Rule 16 is responsible for inserting domain values from superproperties to the subproperties too. It locates a property object named ?p1 which is subproperty of a property ?p and inserts every domain value of ?p into the domain list of ?p1, if does not exist. In that way, every subproperty has in the end that domain values of its superproperties.

Rule 17 has the same functionality to the Rule 16, but it handles range values from superproperties.

Rule 18 handles cases where a property has multiple domain class types. The rule finds a property object that has more than one values in its domain slot and in the body, it calls the function insert-one-domain. This function tries to create a single class from the values in $?D. Firstly it checks all the values in $?D in order to determine the most specific classes, i.e. for classes that are hierarchically related, only the subclasses will be hold. If in the end again more one classes are left, then the system creates dynamically a class subclass of the remaining classes and this class becomes the new domain value for the property ?p.

Rule 19 operates in the same way to rule 18, but handles multiple range values.

Rule 20 is responsible for inserting slot into the corresponding created classes. The rule finds a property meta-object named ?p and holds in the lists $?D and $?R the domain and range values. Then it checks of the property does not exist in the corresponding domain class and with the function insert-property, it creates the property into the class denoted by the domain list $?D. The value of the range list $?R is used in order to determine the type of the property. For object properties, the slot is characterized as INSTANCE-NAME type in order to denote that this slot takes object as values. For datatype properties, there is the corresponding type value, for example for integers there is the INTEGER type value, etc.