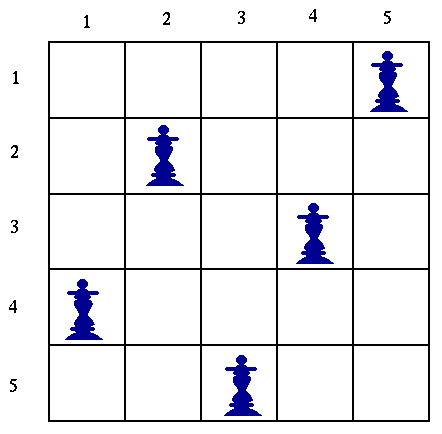
Το πρόβλημα που θα περιγράψουμε στην συνέχεια είναι η τοποθέτηση Ν βασιλισσών σε μια σκακιέρα ΝxΝ, χωρίς να απειλούν η μια την άλλη. Αποτελεί ένα κλασσικό παράδειγμα προβλήματος στην Prolog και συχνά χρησιμοποιείται σαν μετροπρόγραμμα (benchmark) για την μέτρηση της απόδοσης διαφόρων υλοποιήσεων της γλώσσας. Μια λύση του προβλήματος φαίνεται στο επόμενο σχήμα.

Η αναπαράσταση που θα χρησιμοποιήσουμε για την επίλυση του πρβλήματος είναι σχετικά απλή. Οι θέσεις των βασιλισσών αναπαρίστανται από μια λίστα ακεραίων. Ο κάθε ακέραιος αντιπροσωπεύει την σειρά στην οποία τοποθετείται μια βασίλισσα, θεωρόντας δεδομένο ότι τοποθετούνται σε διαφορετικές στήλες. Έτσι η παραπάνω λύση αναπαρίσταται σαν λίστα ακεραίων [4,2,5,3,1].
Το κατηγόρημα queens/2 επιστρέφει την θέση Ν βασιλισσών σε μια σκακιέρα ΝxΝ.Οι θέσεις των βασιλισσών επιστρέφονται σε μια λίστα ακεραίων (Qs), όπως περιγράφηκε παραπάνω.
%%% queens/2
%%% queens(N,Qs)
queens(N, Qs) :-
range(1, N, Ns),
queens(Ns, [], Qs).
Δημιουργεί μια λίστα διαδοχικών ακεραίων από Ν έως Κ, που αντιπροσωπεύει τις βασίλισσες για οι οποίες δεν έχουν τοποθετηθεί ακόμη.
%%% range/2
%%% range(N,K,List)
range(N, N, [N]) :- !.
range(M, N, [M|Ns]) :-
M < N,
M1 is M+1,
range(M1, N, Ns).
Το επόμενο κατηγόρημα αποτελεί το βασικό κατηγόρημα αναζήτησης λύσης του Ν Queens. Η λίστα UnplacedQs περιέχει τις βασίλισσες οι οποίες δεν έχουν ακόμη τοποθετηθεί, η λίστα SafeQs, είναι η λίστα με τις βασίλισσες οι οποίες έχουν τοποθετηθεί και δεν απειλούν η μια την άλλη, ενώ η Qs είναι η λίστα με τις τελικές θέσεις των βασιλισσών (λύση του προβλήματος). Πρώτα επιλέγεται μια βασίλισσα από την λίστα των βασιλισσών που δεν έχουν τοποθετηθεί ακόμη (select/3), ελέγχεται ότι αυτή δεν απειλεί άλλες βασίλισσες (not_attack/2) και τέλος καλείται αναδρομικά μέχρι να μείνει κενή η λίστα με τις μη τοποθετημένες βασίλισσες.
%%% queens/3
%%% queens(UnplacedQs,SafeQs,Qs)
queens([], Qs, Qs).
queens(UnplacedQs, SafeQs, Qs) :-
select(UnplacedQs, UnplacedQs1,
Q),
not_attack(SafeQs, Q),
queens(UnplacedQs1,
[Q|SafeQs], Qs).
Το κατηγόρημα not_attack/2 ελέγχει αν η νέα βασίλισσα είναι σε θέση που αν απειλεί (ή αν απειλείται) από τις υπόλοιπες (Listof_Placed_Queens). Ουσιαστικά καλεί το κατηγόρημα not_attack/3 το οποίο κάνει τον έλεγχο.
%%% not_attack/2
%%% not_acttack(Listof_Placed_Queens,NewQueen).
not_attack(Xs, X) :-
not_attack(Xs, X, 1).
Ελέγχει αν η νέα βασίλισσα είναι σε θέση που αν απειλεί (ή αν απειλείται) από τις υπόλοιπες (Listof_Placed_Queens). Η μεταβλητή Ν καθορίζει το τετράγωνο της διαγωνίου της σκακιέρας (απόσταση από το Χ πάνω στη διαγώνιο) το οποίο ελέγχεται.
%%% not_attack/3
%%% not_acttack(Listof_Placed_Queens,NewQueen,Ν).
not_attack([], _, _) :- !.
not_attack([Y|Ys], X, N) :-
X =\= Y+N, X =\=
Y-N,
N1 is N+1,
not_attack(Ys, X, N1).
Το κατηγόρημα πετυχαίνει όταν η λίστα NewList είναι η List αφαιρώντας από αυτή το στοιχείο X.
%%% select/3
%%% select(List,NewList,X)
select([X|Xs], Xs, X).
select([Y|Ys], [Y|Zs], X) :- select(Ys, Zs, X).
Ένα παράδειγμα εκτέλεσης. Η πρώτη λύση αντιστοιχεί στο σχήμα 1.
| ?- queens(5,L).
L = [4,2,5,3,1] ;
L = [3,5,2,4,1] ;
L = [5,3,1,4,2] ;
L = [4,1,3,5,2] ;
L = [5,2,4,1,3] ;
L = [1,4,2,5,3] ;
L = [2,5,3,1,4] ;
L = [1,3,5,2,4] ;
L = [3,1,4,2,5] ;
L = [2,4,1,3,5] ;
no