Επόμενη: SLD -Ανάλυση Πάνω Επίπεδο: Ανάλυση Προηγούμενη: Ενοποίηση

4.5 Η Αρχή της Ανάλυσης

Η αρχή της ανάλυσης είναι ένας κανόνας παραγωγής της λογικής πρώτης τάξης. Σύμφωνα μ' αυτόν, από δύο προτάσεις C₁ και C₂, μπορούμε να πάρουμε το αναλυθέν (resolvent) τους. Η βασική ιδέα πίσω από την αρχή της ανάλυσης, είναι αυτή της ενοποίησης.

Μια από τις σπουδαιότερες αποδεικτικές διαδικασίες βασίζεται στον κανόνα της ανάλυσης (resolution rule). Ο κανόνας αυτός παράγει το αναλυθέν από τις υποθέσεις και . Για παράδειγμα, αν ξέρουμε ότι

1. Ο Γιάννης προγραμματίζει σε Pascal ή ο Γιάννης προγραμματίζει σε Prolog,
2. Ο Γιάννης δεν προγραμματίζει σε Pascal,

τότε μπορούμε να συμπεράνουμε ότι

Ο Γιάννης προγραμματίζει σε Prolog.

Στο προηγούμενο παράδειγμα, αν θέσουμε Ο Γιάννης προγραμματίζει σε Prolog και Ο Γιάννης προγραμματίζει σε Pascal, τότε μπορούμε να γράψουμε .

Γενικά, το σχήμα το οποίο παράγει ένα αναλυθέν από δύο υποθέσεις και , μπορεί να θεωρηθεί ως ένας κανόνας:

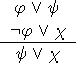
Η αποδεικτική διαδικασία που βασίζεται στον προηγούμενο κανόνα ονομάζεται ανάλυση (resolution) και παρουσιάστηκε για πρώτη φορά το 1965 από τον J.A. Robinson. Η ανάλυση μπορεί να εφαρμοστεί σε όλα τα είδη των τύπων, αλλά συνήθως περιορίζεται στις προτάσεις.

Για να μπορέσουμε να εφαρμόσουμε την ανάλυση σε προτάσεις, χρειαζόμαστε δύο προτάσεις που να περιέχουν ένα συμπληρωματικό ζεύγος, όπως το . Γενικά, αν L₁ είναι ένα θετικό λεκτικό στοιχείο και L₂ ένα αρνητικό, τότε τα L₁ και L₂ συγκροτούν ένα συμπληρωματικό ζεύγος, αν .

Αν έχουμε δύο προτάσεις που περιέχουν ένα συμπληρωματικό ζεύγος, ακολουθώντας το σχήμα της ανάλυσης μπορούμε να πάρουμε μια πρόταση που να περιέχει όλα τα λεκτικά στοιχεία των δύο αρχικών προτάσεων, εκτός από αυτά του συμπληρωματικού ζεύγους. Η με τον τρόπο αυτό σχηματισμένη πρόταση ονομάζεται δυαδικό αναλυθέν (binary resolvent) των δύο αρχικών προτάσεων. Στην περίπτωση κατά την οποία οι προτάσεις περιέχουν από ακριβώς ένα λεκτικό στοιχείο, το δυαδικό αναλυθέν ενδέχεται να είναι η κενή πρόταση 0.12cm.

Ας είναι τώρα ένα σύνολο προτάσεων που θα τις ονομάζουμε και προτάσεις εισόδου (input clauses). Θα ονομάζουμε παραγωγή (derivation) ή αναγωγή (deduction) μιας πρότασης C από το , μια ακολουθία προτάσεων

τέτοια ώστε C=C_n και κάθε C_i είναι είτε κάποιο στοιχείο του είτε το αναλυθέν κάποιων προηγούμενων προτάσεων στην ακολουθία. Θα λέμε ότι η C παράγεται από το (παραγόμενη πρόταση). Μια παραγωγή της κενής πρότασης από το , θα ονομάζεται άρνηση (refutation) του .

Η αναζήτηση για μια απόδειξη είναι αρκετά επίπονη διαδικασία, διότι στην ανάλυση χωρίς περιορισμούς επιτρέπεται η ανάλυση δύο οποιονδήποτε προτάσεων. 'Ετσι, σε κάθε βήμα υπάρχει ένας μεγάλος αριθμός εναλλακτικών αναλύσεων, οι οποίες πρέπει να δοκιμαστούν όλες. Ο αριθμός αυτός μπορεί να ελαττωθεί θέτοντας περιορισμούς στις επιτρεπτές παραγωγές και μάλιστα χωρίς να θυσιάσουμε την πληρότητα (completeness). Τούτο σημαίνει ότι οποιαδήποτε πρόταση η οποία είναι λογικό συμπέρασμα των υποθέσεων, θα εξακολουθεί να μπορεί να παραχθεί.

Πολλές βελτιώσεις έχουν γίνει, από την πρώτη παρουσίαση της αρχής της ανάλυσης από τον Robinson, το 1965. Η σπουδαιότερη από αυτές είναι η σημασιολογική ανάλυση (semantic resolution), που προτάθηκε από τον Slage, καθώς και η γραμμική ανάλυση (linear resolution), που αναπτύχθηκε ανεξάρτητα από τους Loveland και Luckham. Η γραμμική ανάλυση είναι απλούστερη της σημασιολογικής και χαρακτηρίζεται από τη γραμμικότητα του χώρου των παραγωγών της. Στην γραμμική ανάλυση, τουλάχιστον μία από τις γονικές προτάσεις σε κάθε απόπειρα ανάλυσης πρέπει να είναι είτε πρόταση εισόδου, είτε προγενέστερη της γονικής. Μια σημαντική, επιπρόσθετη βελτίωση, ονομάζεται SL- ανάλυση, δηλαδή γραμμική (Linear) ανάλυση με στρατηγική επιλογής (Selection) και προτάθηκε από τους Kowalski και Kuehner.